"The woods, lovely, dark and deep, are to be seen on foot."

the radiation equilibrium is classical

(h is classical)

sheet1

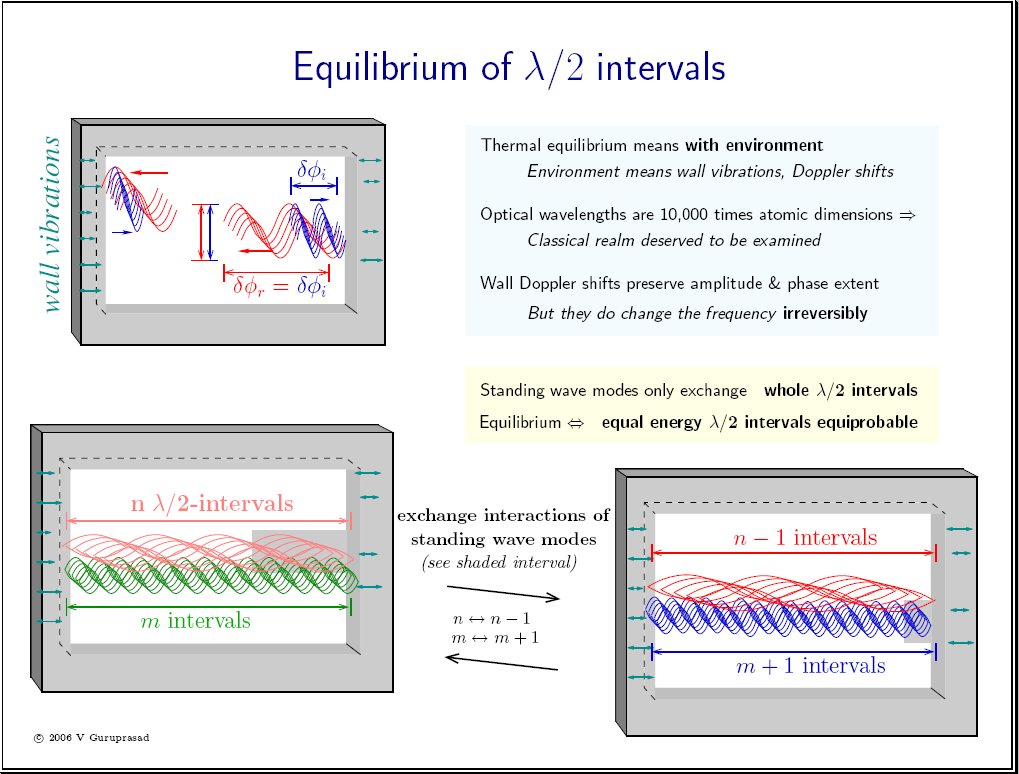
sheet2

link to Planck's paper

link to PhysicsWeb article

Below is an approximate rendition of my verbal explanation to at least 10 groups of visitors at the APS Poster Session, plus a few senior physicists outside of the session. Please also see the "full paper" (slightly dated: physics/0003041). Comments are respectfully solicited.

Layman explanation

Planck's law E = h ν holds for standing waves in thermal equilibrium [sheet2 top right, click to enlarge]. What else is proportional to the frequency ν? The number of peaks is also proportional to the frequency in any standing wave! This is mathematical, goes with the definition of standing waves. [sheet1 bottom]. So Planck's law implies that the equilibrium standing wave "peaks" (more precisely, λ/2 intervals around the peaks) carry equal expectation energies in equilibrium.

But Planck could not have justified any such classical equilibrium, as he couldn't even explain how energized standing waves "thermalize", i.e. how their energy disperses into multiple modes to form heat and how they reach equilibrium. In 1897, when Planck was trying to derive Wien's law, Boltzmann "demolished" Planck's attempts to find an explanation by pointing out that the symmetry of electrodynamics prohibited irreversible mixing of the wave energies [see the PhysicsWeb article - Section Black-body radiation paragraph 1]. This forced Planck to postulate a a principle of elementary disorder that did not depend on mechanics or electrodynamics [paragraph 4 in the same article]!

But 1897 was also when Steinmetz's book Theory and Calculation of Alternating Current Phenomena (with Ernst J Berg) appeared - the material having been presented earlier at the International Electrical Congress in 1893 [see wikipedia & detailed links, for instance]. This was the theory of how to calculate the energies of alternating current waveforms, and presumably necessary for computing the energies of travelling and standing waves. Wave energies were thus a relatively new concept and Planck and Boltzmann, like other physicists of the time, were simply not equipped to think of an equilibrium of wave energies by themselves. In both Planck's and the Rayleigh-Jeans theory published in 1905, the equilibrium envisaged is that driven by matter interactions, suggesting the incorrect equipartition of kT/2 to each mode (which obviously blows up because there are infinite modes).

Looking closely at the equilibrium condition for standing waves [sheet1], it becomes clear that Boltzmann had in fact made a mistake all along even in his kinetic theory, since he had failed to consider the thermal motions of the walls. Boltzmann did not have to consider the wall motions for two reasons:

before the kinetic theory, there was very little understanding of the thermal motions, so accounting for wall motions would have posed distracting conceptual difficulties; and
the large number of molecules was sufficient for his statistical theory.

It is only with the radiation spectrum that this becomes a difficulty: the number of standing wave modes is even larger, infinite to be precise, but standing waves by themselves, faced with perfectly rigid walls, cannot "mix" by definition. Observe, however, that perfectly rigid walls can only represent absolute zero temperature, and at T = 0 K, not mixing is precisely what we do want, by the Nernst theorem - the 3rd law of thermodynamics - which requires all motion to be frozen into a few specific states. In retrospect, this finally also "explains" the Fermi-Pasta-Ulam problem that large body simulations still lead to large chaotic periodicities. Conversely, for equilibrium at any temperature T > 0, we do need to consider walls also at this temperature, hence moving under thermal forces. Their Doppler shifts then suffice to produce irreversible mixing because each wavetrain will keep getting shifted in frequency in a truly random sequence.

Thus we can now explain, with our modern hindsight, a classical equilibrium of standing waves, and arrive at a Boltzmann distribution over the "peaks". This happens to be just the right ingredient for deriving Planck's spectrum [sheet2], which requires a Boltzmann probability for each oscillator state that in turn corresponds to the observed standing wave mode or one of its harmonics. Not only that, but recall from Physics 101 that the form of the spectrum suffices to make E_λ/2, the interval expectation energy, a universal constant. If you don't remember that, just consider two cavities with arbitrary geometries and volumes in equilibrium with each other. As the denominator is dimensionless, the numerators must match at each frequency ν - this is known as the principle of detailed balance - hence the remaining numerator factor E_λ/2 must be a universal constant.

Finally, we need to also explain why our measurements are consistent with the standing wave distribution (Planck's) rather than with the λ/2 intervals distribution (which is Boltzmann) - this is given in sheet2. It incidentally also eliminates the possibility of retaining inherently nonclassical semantics like zero-point energy in physics, as explained in my submitted paper.

QED (!)

Sheet 1

Sheet 2

Last change: 2006.04.22 21:53:30. papers licensing news contact Please revisit - this site & i continue to evolve.